Low voltage ride through
In electric power systems, low-voltage ride through (LVRT), or fault ride through (FRT), sometimes under-voltage ride through (UVRT), is the capability of electric generators to stay connected in short periods of lower electric network voltage (cf. voltage dip). It is needed at distribution level (wind parks, PV systems, distributed cogeneration, etc.) to avoid that a short circuit on HV or EHV level will lead to a wide-spread loss of generation. Similar requirements for critical loads such as computer systems and industrial processes are often handled through the use of an uninterruptible power supply (UPS) or capacitor bank to supply make-up power during these events.
General concept
Many generator designs use electric current flowing through windings to produce the magnetic field on which the motor or generator operates. This is in contrast to designs that use permanent magnets to generate this field instead. Such devices may have a minimum working voltage, below which the device does not work correctly, or does so at greatly reduced efficiency. Some will cut themselves out of the circuit when these conditions apply. This effect is more severe in doubly-fed induction generators (DFIG), which have two sets of powered magnetic windings, than in squirrel-cage induction generators which have only one. Synchronous generators may slip and become unstable, if the voltage of the stator winding goes down below a certain threshold.
Risk of chain reaction
In a grid containing many distributed generators subject to a low-voltage disconnection, it is possible to cause a chain reaction that takes other generators offline as well. This can occur in the event of a voltage dip that causes one of the generators to disconnect from the grid. As voltage dips are often caused by too little generation for the load in a distribution grid, removing generation can cause the voltage to drop further. This may bring the voltage down enough to cause another generator to trip, lower the voltage even further, and may cause a cascading failure.
Ride through systems
Modern large-scale wind turbines, typically 1 MW and larger, are normally required to include systems that allow them to operate through such an event, and thereby “ride through” the low voltage. Similar requirements are now becoming common on large solar power installations that likewise might cause instability in the event of a disconnect. Depending on the application the device may, during and after the dip, be required to:
disconnect temporarily from the grid, but reconnect and continue operation after the dip
stay operational and not disconnect from the grid
stay connected and support the grid with reactive power (defined as the reactive current of the positive sequence of the fundamental)
Standards
A variety of standards exist and generally vary across jurisdictions. Examples of the such grid codes are the German BDEW grid code and its supplements 2, 3, and 4 as well as the National Grid Code in UK.
Testing
Testing of the devices with less than 16 Amp rated current is described in the standard IEC 61000-4-11 and for higher current devices in IEC 61000-4-34. For wind turbines the LVRT testing is described in the standard IEC 61400-21 (2nd edition August 2008). More detailed testing procedures are stated in the German guideline FGW TR3 (Rev.22).
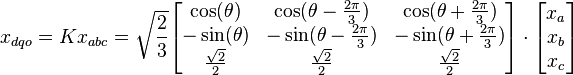
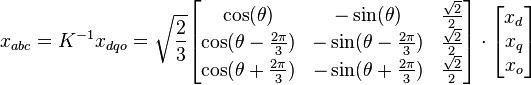

 ,
, .
.
 ):
):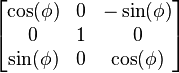 ,
,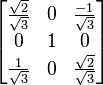 .
.
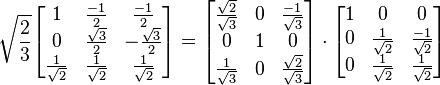

 .
.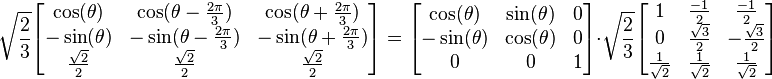 .
.
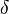 . The d-q axis is shown rotating with angular velocity equal to
. The d-q axis is shown rotating with angular velocity equal to  , the same angular velocity as the phase voltages and currents. The d axis makes an angle
, the same angular velocity as the phase voltages and currents. The d axis makes an angle 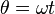 with the A winding which has been chosen as the reference.The currents
with the A winding which has been chosen as the reference.The currents 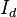 and
and 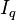 are constant DC quantities.
are constant DC quantities.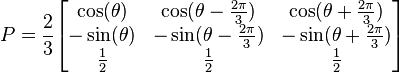
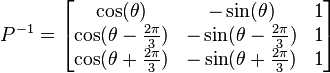
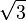 .
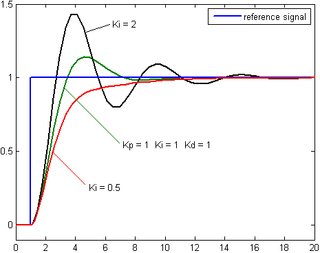
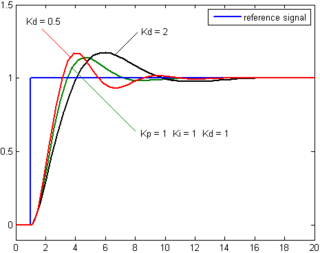
.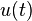 as the controller output, the final form of the PID algorithm is:
as the controller output, the final form of the PID algorithm is: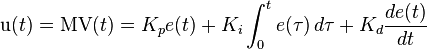
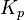 : Proportional gain, a tuning parameter
: Proportional gain, a tuning parameter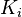 : Integral gain, a tuning parameter
: Integral gain, a tuning parameter : Derivative gain, a tuning parameter
: Derivative gain, a tuning parameter : Error
: Error 
 : Set Point
: Set Point : Process Variable
: Process Variable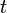 : Time or instantaneous time (the present)
: Time or instantaneous time (the present) : Variable of integration; takes on values from time 0 to the present
: Variable of integration; takes on values from time 0 to the present 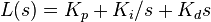
 : complex number frequency
: complex number frequency
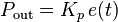



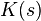 : PID transfer function
: PID transfer function : Plant transfer function
: Plant transfer function . Typically, this happens when
. Typically, this happens when 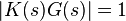 with a 180 degree phase shift. Stability is guaranteed when
with a 180 degree phase shift. Stability is guaranteed when  for frequencies that suffer high phase shifts. A more general formalism of this effect is known as the
for frequencies that suffer high phase shifts. A more general formalism of this effect is known as the 